Arcos de Málaga: rebajado

Ya tenemos aquí la segunda entrega del serial 'Arcos de Málaga' que comencé hace un mes con el arco romano o de medio punto, que por cierto ha tenido cierta aceptación, puesto que dicha entrada ha sido la quinta más votada en la pasada Edición 5.8 Betty Scott del Carnaval de Matemáticas.

Hoy os presento un nuevo arco que está directamente relacionado con el romano y que, por lo tanto, también es bastante sencillo de construir. Os estoy hablando del arco rebajado, cuya presencia en edificios y monumentos de nuestras ciudades es muy evidente como comprobaréis más tarde, pero primero vamos a ver qué pasos hay que seguir para construirlo:

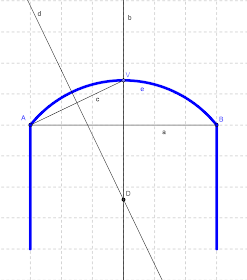
1. Elegimos dos puntos A y B para determinar el segmento a que une ambos puntos.
2. Trazamos la mediatriz b del segmento anterior, de tal forma que obtenemos un punto de corte C.
3. Elegimos un vértice V sobre la mediatriz b, obteniendo así el segmento c que une dicho punto con el A.
4. Al segmento anterior le trazamos la mediatriz d, que se corta con la mediatriz b en el punto D.
5. Con centro en D trazamos un arco de circunferencia e de radio el segmento DA con inicio en el punto A y fin en el punto B, y que obviamente también pasará por el vértice V. De esta forma, obtenemos el arco rebajado.

Sencillo, ¿verdad? Si os dais una vuelta por la ciudad en la que vivís, estoy seguro de que os toparéis con más de un arco rebajado en casi cada calle por la que paséis. En el caso de mi ciudad, Málaga, hay bastantes y variados ejemplos, algunos de los cuales os muestro a continuación.

Calle San Agustín (detalle de un portal)

Casa Hermandad de la cofradía de El Rico

Jardines de Pedro Luis Alonso

Palacio Episcopal

Esquina de las calles San Agustín y Duque de la Victoria

Pues nada más por hoy. Únicamente me queda invitaros a participar en esta entrada dando a conocer los arcos rebajados de los sitios en los que vivís, y ya de paso aprovecho para desearos una Feliz Navidad y un Próspero Año Nuevo 2015.

Nota: este post forma parte del Carnaval de Matemáticas, que en esta cuadragésima novena edición, también denominada 5.9 Emma Castelnuovo, está organizado por Elisa Benítez a través de su blog Que no te aburran las M@TES.