Empezamos dos milenios antes del nacimiento de Jesucristo con los sistemas de numeración que crearon los babilonios y los egipcios. Luego, nos introdujimos en las civilizaciones griega, etrusca y romana para conocer los símbolos que utilizaban para los números. En todos los casos, hemos echado en falta el cero, pero hoy por fin nuestro viaje se encontrará con ese trazo redondeado que tanto utilizamos y que tanto nos facilita las cosas. Muchos siglos han tenido que pasar, pero ¿quién dijo que esto era sencillo?
Si a alguien le debemos el que actualmente usemos los números que conocemos es a los indios, puesto que es a partir de los símbolos que ellos idearon sobre el siglo III a. C. de donde hemos diseñado los dígitos actuales. Por aquel entonces, los hindúes le habían asignado un símbolo a los números del 1 al 9, que son los que aparecen en la imagen superior, pero también tenían trazos 'personalizados' para el 10, el 20, el 30, y así sucesivamente hasta el 90; luego, otros nueve símbolos para el 100, el 200, el 300... y el 900; también para el 1.000, el 2.000, el 3.000... y el 9.000; y así sucesivamente. Con estos símbolos podían representar cualquier número que quisieran, empleando para tal caso un sistema aditivo que consistía en poner los símbolos necesarios en orden descendente según su valor. Por ejemplo, para escribir el 7.915 ponían primero el símbolo del 7.000, luego el del 900, después el del 10 y por último el del 5. Así pues, este sistema era idéntico al de la numeración jónica que analizamos en la entrega anterior, y muy similar también a la egipcia que estudiamos en la primera entrada de esta serie.
No cabe duda que los sistemas aditivos son un poco enfarragosos por la gran cantidad de símbolos que hay que saberse para poder representar cualquier cantidad. Los hindúes se dieron cuenta de ello, y poco a poco se fueron mudando a la notación posicional, que es otra de los conceptos matemáticos que hemos heredado de esta civilización. A pesar de escribir los números como hemos comentado, los indios llevaban a cabo las operaciones elementales con una determinada cantidad de fichas separadas por líneas verticales para indicar cuántas unidades, decenas, centenas, unidades de millar, etc., del número en cuestión. Estas fichas se cambiaron posteriormente por los nueve símbolos de la imagen de arriba, por lo que ahora cada dígito tenía un valor diferente en función de la posición que ocupara dentro del número. Siguiendo con el ejemplo anterior, el 5 representa cinco unidades, pero si estuviera en la posición de las decenas representaría el cincuenta, el quinientos en caso de ser la tercera cifra por la derecha, etc.
¿Qué problema había? Pues que no tenían ningún símbolo para indicar la ausencia de unidades, decenas o cualquier otra potencia de diez si hiciera falta en un determinado número, es decir, necesitaban representar la nada, el cero. Ahora nos parece algo normal y lógico, pero la invención del cero supuso un antes y un después en la historia de la aritmética, y por consiguiente de las matemáticas. Corría el siglo V o VI d. C. cuando a los indios no se les ocurrió una manera mejor de simbolizar la nada que con un círculo vacío. ¿Se os hubiera ocurrido a vosotros algún símbolo más ilustrativo que ése?
Así pues, los hindúes fueron los precursores del sistema de numeración que usamos hoy día, pero realmente fueron los árabes los encargados de traernos esta notación numérica tan avanzada y sencilla. En el siglo VIII, tras haber conquistado la India, los árabes se quedaron prendados de su sistema para escribir y manipular números, así que lo adoptaron y lo difundieron por todos sus territorios, desde Asia a la Península Ibérica, pasando por el norte de África. Y de rebote, ya en plena Edad Media, llegó a Europa, donde todavía se seguían usando los numerales romanos. Uno de los grandes artífices de que la notación arábiga fuese aceptada poco a poco por los europeos fue Fibonacci, sí, el de la famosa secuencia 1, 1, 2, 3, 5, 8, 13, 21, etc. Durante una de sus visitas al norte de África, este matemático italiano descubrió la numeración indoarábiga, que le resultó muy sencilla y muy útil para la contabilidad y otras situaciones comerciales de aquellos tiempos, y así lo dejó por escrito en su obra Liber Abaci. Su influencia hizo que la aceptación de este sistema fuera notable, aunque hubo quienes en un principio se resistieron a cambiar sus métodos habituales de cálculo, como por ejemplo los mercaderes, que preferían la numeración romana. No fue hasta el siglo XVIII cuando se asentaron definitivamente los diez dígitos que se muestran arriba, denominados números arábigos, los cuales guardan un gran parecido a los originales de la India.
Hasta ahora, durante este viaje por la historia de los números nos hemos movido por Europa, África y Asia, pero ¿y al otro lado del Atlántico? Los habitantes del continente americano también desarrollaron sus propios sistemas de numeración antes de que los europeos descubrieran sus tierras, y uno de ellos ha cobrado una gran relevancia: la numeración maya. ¿Los mayas? ¿Esos que dicen que el mundo se acaba este mismo año, en 2012? Sí, esos mismos, así que, si tú eres de los que se creen esta profecía, aprovecha los días que te quedan y quédate aquí leyendo lo que queda de esta entrada.
Los mayas sustentaron su sistema de numeración en la base 20, la cual puede tener su origen en el número de dedos que tiene cada persona entre sus manos y sus pies; de hecho, así lo parece a tenor de la manera en la que representaban los primeros veinte números. Fijaos en la imagen de la derecha y observad que los números del 1 al 4 se simbolizan con tantos puntos (¿los dedos de una mano?) como indica el valor, mientras que el 5 se representa con una línea (¿una mano?). Del 6 al 9 se añaden puntos a dicha línea (¿una mano y los dedos de la otra mano?), y el 10 serían dos líneas (¿dos manos?). Hasta el 19 se procede de la misma forma, es decir, un punto representaría un dedo suelto y una línea sería una mano o un pie entero. El sistema de numeración maya es aditivo porque el valor de cada número se obtiene de sumar el valor que representa cada uno de los símbolos que lo componen (el punto es una unidad y la raya son cinco), pero también es posicional, por lo que a partir del número 20 se añade un nuevo orden para indicar las 'veintenas' o grupos de veinte unidades que se llevan contadas, de la misma forma que nosotros usamos las decenas, pero ellos no escribían los números en horizontal, sino en vertical. Por ejemplo, el número 72 se representaría con tres puntos en el primer nivel (3*20 = 60) y dos puntos y dos rayas en el segundo nivel (2 + 5 + 5 = 12), de donde se obtiene por consiguiente que 60 + 12 = 72.
¿Y ese símbolo tan extraño que aparece en la parte superior de la imagen? Sí, es el cero de los mayas, una especie de concha o caracol cuya invención se cree que es más antigua incluso que el cero de los hindúes, pues ciertos estudios indican que su primer uso data del primer siglo antes de nuestra era. Así pues, podemos decir que, mientras se demuestre lo contrario, el cero nació en América, aunque en realidad el símbolo que usamos hoy día es el que nos legaron los indios a través de los árabes.
Nuestro viaje a través de la historia de los números ya está a punto de terminar. En la próxima entrega de esta serie daremos por finalizado el viaje, así que estad atentos.
Nota: este post forma parte del Carnaval de Matemáticas, que en esta vigesimotercera edición, también denominada 3.141, está organizado por Rafael Ballesteros a través de su blog DesEquiLIBROS.
Si a alguien le debemos el que actualmente usemos los números que conocemos es a los indios, puesto que es a partir de los símbolos que ellos idearon sobre el siglo III a. C. de donde hemos diseñado los dígitos actuales. Por aquel entonces, los hindúes le habían asignado un símbolo a los números del 1 al 9, que son los que aparecen en la imagen superior, pero también tenían trazos 'personalizados' para el 10, el 20, el 30, y así sucesivamente hasta el 90; luego, otros nueve símbolos para el 100, el 200, el 300... y el 900; también para el 1.000, el 2.000, el 3.000... y el 9.000; y así sucesivamente. Con estos símbolos podían representar cualquier número que quisieran, empleando para tal caso un sistema aditivo que consistía en poner los símbolos necesarios en orden descendente según su valor. Por ejemplo, para escribir el 7.915 ponían primero el símbolo del 7.000, luego el del 900, después el del 10 y por último el del 5. Así pues, este sistema era idéntico al de la numeración jónica que analizamos en la entrega anterior, y muy similar también a la egipcia que estudiamos en la primera entrada de esta serie.
No cabe duda que los sistemas aditivos son un poco enfarragosos por la gran cantidad de símbolos que hay que saberse para poder representar cualquier cantidad. Los hindúes se dieron cuenta de ello, y poco a poco se fueron mudando a la notación posicional, que es otra de los conceptos matemáticos que hemos heredado de esta civilización. A pesar de escribir los números como hemos comentado, los indios llevaban a cabo las operaciones elementales con una determinada cantidad de fichas separadas por líneas verticales para indicar cuántas unidades, decenas, centenas, unidades de millar, etc., del número en cuestión. Estas fichas se cambiaron posteriormente por los nueve símbolos de la imagen de arriba, por lo que ahora cada dígito tenía un valor diferente en función de la posición que ocupara dentro del número. Siguiendo con el ejemplo anterior, el 5 representa cinco unidades, pero si estuviera en la posición de las decenas representaría el cincuenta, el quinientos en caso de ser la tercera cifra por la derecha, etc.
¿Qué problema había? Pues que no tenían ningún símbolo para indicar la ausencia de unidades, decenas o cualquier otra potencia de diez si hiciera falta en un determinado número, es decir, necesitaban representar la nada, el cero. Ahora nos parece algo normal y lógico, pero la invención del cero supuso un antes y un después en la historia de la aritmética, y por consiguiente de las matemáticas. Corría el siglo V o VI d. C. cuando a los indios no se les ocurrió una manera mejor de simbolizar la nada que con un círculo vacío. ¿Se os hubiera ocurrido a vosotros algún símbolo más ilustrativo que ése?
Así pues, los hindúes fueron los precursores del sistema de numeración que usamos hoy día, pero realmente fueron los árabes los encargados de traernos esta notación numérica tan avanzada y sencilla. En el siglo VIII, tras haber conquistado la India, los árabes se quedaron prendados de su sistema para escribir y manipular números, así que lo adoptaron y lo difundieron por todos sus territorios, desde Asia a la Península Ibérica, pasando por el norte de África. Y de rebote, ya en plena Edad Media, llegó a Europa, donde todavía se seguían usando los numerales romanos. Uno de los grandes artífices de que la notación arábiga fuese aceptada poco a poco por los europeos fue Fibonacci, sí, el de la famosa secuencia 1, 1, 2, 3, 5, 8, 13, 21, etc. Durante una de sus visitas al norte de África, este matemático italiano descubrió la numeración indoarábiga, que le resultó muy sencilla y muy útil para la contabilidad y otras situaciones comerciales de aquellos tiempos, y así lo dejó por escrito en su obra Liber Abaci. Su influencia hizo que la aceptación de este sistema fuera notable, aunque hubo quienes en un principio se resistieron a cambiar sus métodos habituales de cálculo, como por ejemplo los mercaderes, que preferían la numeración romana. No fue hasta el siglo XVIII cuando se asentaron definitivamente los diez dígitos que se muestran arriba, denominados números arábigos, los cuales guardan un gran parecido a los originales de la India.
Hasta ahora, durante este viaje por la historia de los números nos hemos movido por Europa, África y Asia, pero ¿y al otro lado del Atlántico? Los habitantes del continente americano también desarrollaron sus propios sistemas de numeración antes de que los europeos descubrieran sus tierras, y uno de ellos ha cobrado una gran relevancia: la numeración maya. ¿Los mayas? ¿Esos que dicen que el mundo se acaba este mismo año, en 2012? Sí, esos mismos, así que, si tú eres de los que se creen esta profecía, aprovecha los días que te quedan y quédate aquí leyendo lo que queda de esta entrada.
Los mayas sustentaron su sistema de numeración en la base 20, la cual puede tener su origen en el número de dedos que tiene cada persona entre sus manos y sus pies; de hecho, así lo parece a tenor de la manera en la que representaban los primeros veinte números. Fijaos en la imagen de la derecha y observad que los números del 1 al 4 se simbolizan con tantos puntos (¿los dedos de una mano?) como indica el valor, mientras que el 5 se representa con una línea (¿una mano?). Del 6 al 9 se añaden puntos a dicha línea (¿una mano y los dedos de la otra mano?), y el 10 serían dos líneas (¿dos manos?). Hasta el 19 se procede de la misma forma, es decir, un punto representaría un dedo suelto y una línea sería una mano o un pie entero. El sistema de numeración maya es aditivo porque el valor de cada número se obtiene de sumar el valor que representa cada uno de los símbolos que lo componen (el punto es una unidad y la raya son cinco), pero también es posicional, por lo que a partir del número 20 se añade un nuevo orden para indicar las 'veintenas' o grupos de veinte unidades que se llevan contadas, de la misma forma que nosotros usamos las decenas, pero ellos no escribían los números en horizontal, sino en vertical. Por ejemplo, el número 72 se representaría con tres puntos en el primer nivel (3*20 = 60) y dos puntos y dos rayas en el segundo nivel (2 + 5 + 5 = 12), de donde se obtiene por consiguiente que 60 + 12 = 72.
¿Y ese símbolo tan extraño que aparece en la parte superior de la imagen? Sí, es el cero de los mayas, una especie de concha o caracol cuya invención se cree que es más antigua incluso que el cero de los hindúes, pues ciertos estudios indican que su primer uso data del primer siglo antes de nuestra era. Así pues, podemos decir que, mientras se demuestre lo contrario, el cero nació en América, aunque en realidad el símbolo que usamos hoy día es el que nos legaron los indios a través de los árabes.
Nuestro viaje a través de la historia de los números ya está a punto de terminar. En la próxima entrega de esta serie daremos por finalizado el viaje, así que estad atentos.
Nota: este post forma parte del Carnaval de Matemáticas, que en esta vigesimotercera edición, también denominada 3.141, está organizado por Rafael Ballesteros a través de su blog DesEquiLIBROS.

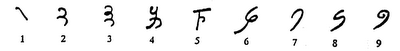


5 comentarios:
¡Qué me gustan a mí estas cosas!
El 0, ese gran desconocido. Que invento tan simple y a la vez tan complicado. Vaya pasada. Me está encantando ir conociendo las historia de los números. Luego puedes hacerlo con las letras, las notas musicales u otra cosa jeje
Pepe E. Carretero: antes de nada, te doy la bienvenida a mi blog, puesto que es la primera vez que me dejas un comentario. Me gustaría saber cómo me has encontrado, si no te importa decírmelo.
Me alegro de que te gusten. Supongo que te habrás leído ya las dos entregas anteriores, y todavía queda la última ;)
Migue: ¿qué sería de nosotros sin el cero? ¿Qué sería de muchos alumnos vagos sin el cero? :P
Ya ves que lo que ahora parece fácil antes no lo era tanto. Sólo queda un capítulo de esta larga historia que estoy tratando de resumir, así que aprovéchala cuando la publique ;)
De lo que propones no haré ninguna historia, aunque sería interesante indagar sobre ello. La historia de las notas musicales creo que sí la conozco, aunque no estoy del todo seguro...
Gracias a los dos por vuestros comentarios ;)
Genial entrada, desconocía la numeración maya y me parece muy interesante, como que seguramente son los inventores del número cero.
Saludos.
Me alegro de que te haya gustado ;)
Yo también desconocía la numeración maya hasta hace muy poco, y la verdad es que es bastante simple para la época de la que estamos hablando, y encima aislados del resto del mundo.
Los inventores oficiales del cero son los indios, más que nada porque conservamos la forma de dicha cifra.
Saludos ;)
Publicar un comentario